Home

By: Danny Martinez Hibbert

Academic Integrity Declaration: I am aware of the requirements of good academic practice and the potential penalties for any breaches. I confirm that this assignment is all my own work.

Introduction

Welcome to my blog dear reader! In this blog post I will be presenting the analysis of collected data from an experiment. Data from the experiment will be analyzed and presented for review and understanding to the reader. This information can be used to understand the application of the law of elasticity on real materials and what your results may look like. All data will be based on Robert Hooke’s law.

Robert Who?

Robert Hooke was a chemist and physicist who solidified the understanding and application of elasticity and its effects on materials based on force applied to a solid body that stretches. This was just one of the many things Hooke is accredited for but in this blog, we will be looking at his found formula on elasticity.

The experiment

The data will be in relation to an experiment in the use of Hooke’s Law and the relationship between the force applied to three elastic materials. All three materials will react differently to the force applied to them, mainly in the extension of the material and the correlation between linear and non-linear results. Hooke’s law allows us to see the properties of elasticity, whether it’s an elastic band or a spring by seeing the relationship between the extension and the force applied.

You will notice the data presented will be very similar but also presents an interesting condition that can be seen from certain materials when stretched beyond their means, Hooke’s law will allow us to understand this relationship as well. All data is presented in graphical form for visual aid.

The image above shows the practical application of the law and what it may look like when a spring is stretched with weighted ends. Notice the spring extends by twice the amount when the weight is doubled in this particular example. This is a linear format. However, it may not always be the case, Hooke’s law is only applicable for the range in which the material is not deformed and able to retract to its original shape.

 “Hooke’s law describes the elastic properties of materials only in the range in which the force and displacement are proportional.” [3]

F = kx

• F = force
• K = spring constant (malleability)
• X = Distance change

So, let’s look at the data!

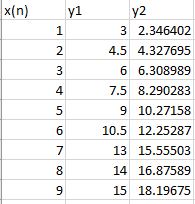
The three different materials are denoted as y1, y2 and z.

X axis represents the force applied and the y axis the amount of deformation

This table shows data for two of the materials that were experimented on. X is the total amount of force applied and Y1, Y2 are the amount of deformation for both of the materials that were tested. The third material will be presented later.

This graph for the first material shows a very consistent and linear relationship between the deformation of the material and the force applied. This will allow us to find variables a and b from y1 = ax + b through transposition.

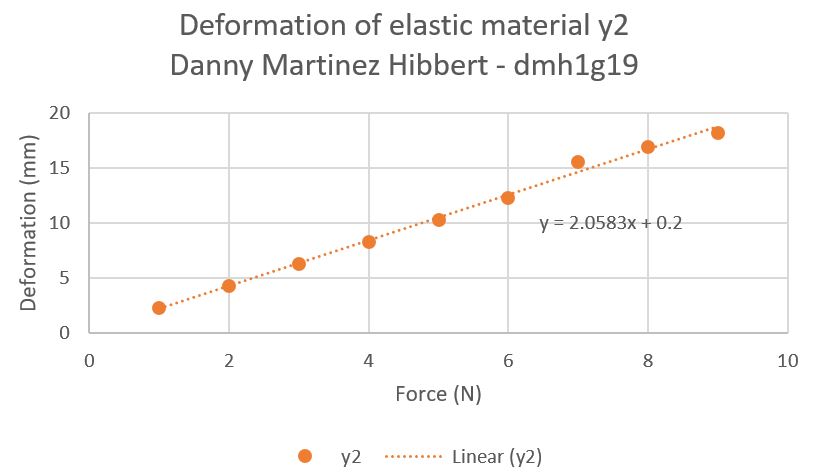
When applying the same force to a different material we see a similar trend in data. Once again it is of a linear form, the increments of force on the elasticity is small and consistent. Material 2 is given by Y2 = (a+0.5)x + c where c = 0.2.

When combining both results together we see the similarity directly and how they are both linear

By looking at the graph we can see both materials cross at a certain point on the graph. From looking at the graph we can estimate that both materials deform the same amount when presented with the same force in Newtons. This can be approximated to 2 Newtons at 4.5 mm of deformation.

y=1.5583x+1.375
0.5x+0.2=1.375
0.5x=1.175
x=2.35

y=2.0583x+0.2
y=(2.0583)(2.35)+0.2
y=5.037005

x=2.35, y=5.037005

To check our answer we can perform a system of equations and rule out needed variables. As above we can see the accurate force in newtons is actually 2.35(N) with 5.03(mm) of deformation.

Transposing formula from the graphed data will allow us to find the values for both the remaining materials. Also the third material can be presented with z =  x^3 +b.

Before moving onto the third material, notice the difference in output from the two initial materials Y1 and Y2. The same force has been applied but the deformation is not exact. This is because each material has its own spring constant, denoted K. This is how much the material will oppose the force being applied to it.

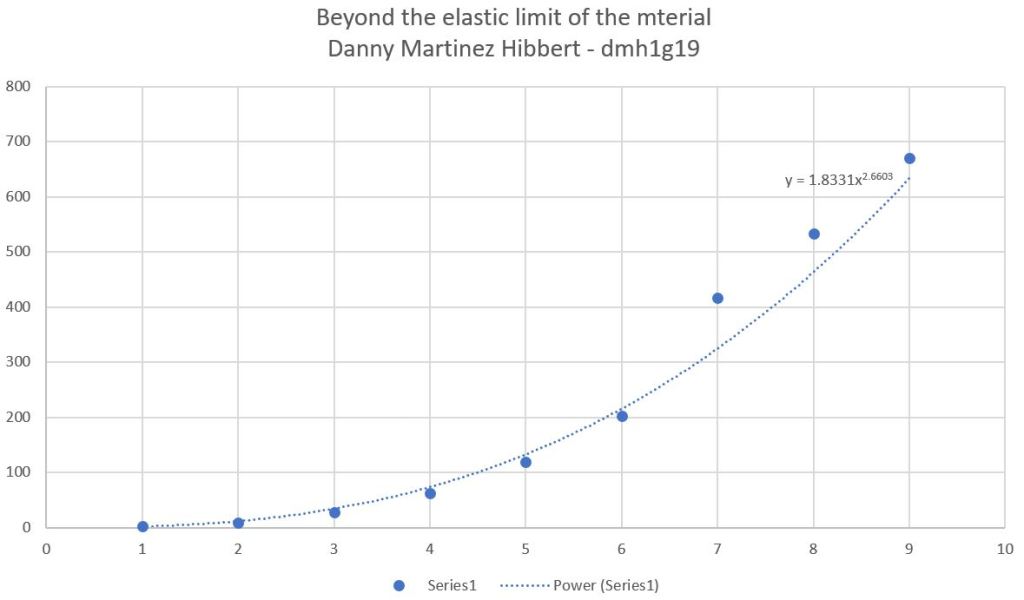
The third material is wildly different, notice how the force applied is not dissimilar to our early applications but the deformation is non-linear! The expectation no longer holds true. Notice how the deformation is much larger now and applying force will create an exponential change. This is where Hooke’s law deceives the viewer, one must not believe the elasticity of all solid bodies are linear in deformation such as x, 2x and so forth. The material used here may be considerably different in size, shape or substance (the spring constant). Hooke’s law is not used on materials with large amount of deformation, in this case the material has passed it’s ‘elastic region’ and becomes non-linear in relationship. The material may no longer revert to its original shape – also known as the ‘yield stress’.

Not everything is perfect…

By looking at the graph for material Y1, there is an inconsistent deformation in the linear nature of the data. It appears as though the material extended too much by a slight amount, this could have been a result of incorrect placement of weight such as too much, or inaccurate measurement in the movement of the material after placing the weight.

A farewell

As you can see Hooke’s law can provide us with very accurate and reliable data when measuring small changes in the deformation of elasticity in solid objects. Thanks for reading my blog, I hope you learned something or found it interesting.

Bibliography: